| Автор |
Сообщение |
monks101
Зарегистрирован: 03.08.2010
Сообщения: 6

|
 Добавлено:
Вт Авг 03, 2010 2:23 pm Добавлено:
Вт Авг 03, 2010 2:23 pm |
  |
*** (delete theme) |
Последний раз редактировалось: monks101 (Ср Авг 18, 2010 10:23 pm), всего редактировалось 1 раз |
|
  |
 |
|
|
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Вт Авг 03, 2010 6:13 pm Добавлено:
Вт Авг 03, 2010 6:13 pm |
  |
А здесь не стоит решать напрямую. Сделайте замену 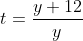 Тогда уравнение Ваше преобразуется к виду Тогда уравнение Ваше преобразуется к виду
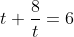
А это уже решается довольно просто. |
|
|
  |
 |
monks101
Зарегистрирован: 03.08.2010
Сообщения: 6

|
 Добавлено:
Вт Авг 03, 2010 7:32 pm Добавлено:
Вт Авг 03, 2010 7:32 pm |
  |
** (delete theme) |
Последний раз редактировалось: monks101 (Ср Авг 18, 2010 10:24 pm), всего редактировалось 2 раз(а) |
|
  |
 |
monks101
Зарегистрирован: 03.08.2010
Сообщения: 6

|
 Добавлено:
Вт Авг 03, 2010 7:51 pm Добавлено:
Вт Авг 03, 2010 7:51 pm |
  |
если не трудно.. еще один пример.
система неравенств.
4х-12<0
-x+a<=0 (знак тут "меньше или равно")
при каких значениях а система имеет 5 целых решений?
буду очень благодарен, если поможете |
|
|
  |
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Вт Авг 03, 2010 9:34 pm Добавлено:
Вт Авг 03, 2010 9:34 pm |
  |
Ну, это тоже несложно :)
Из первого неравенства следует, что x<3.
Из второго неравенства получим: x>=a.
Короче говоря, нам нужно определить параметр а, для которого двойному неравенству a=<x<3 удовлетворяет ровно 5 целочисленных решений. Отсюда получим верхнюю границу для значений параметра a=3-5=-2. |
Последний раз редактировалось: Wolfling (Ср Авг 04, 2010 12:22 am), всего редактировалось 2 раз(а) |
|
  |
 |
monks101
Зарегистрирован: 03.08.2010
Сообщения: 6

|
 Добавлено:
Вт Авг 03, 2010 10:07 pm Добавлено:
Вт Авг 03, 2010 10:07 pm |
  |
лучше этого форума не находил  огромное вам спасибо. огромное вам спасибо.
P.S. а если а<0? т.е. найти все отрицательные значения а, чтобы было 5 целых решений у системы? |
|
|
  |
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Ср Авг 04, 2010 12:20 am Добавлено:
Ср Авг 04, 2010 12:20 am |
  |
Ну, если ставить вопрос о всех действительных значениях параметра а, то очевидно, что эти значения должны принадлежать полуинтервалу ![a\epsilon (-3;-2]](http://latex.codecogs.com/gif.latex?a\epsilon (-3;-2]) Потому что если а будет меньше либо равно -3, то система будет иметь больше пяти решений. Потому что если а будет меньше либо равно -3, то система будет иметь больше пяти решений. |
|
|
  |
 |
|
|


