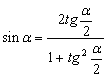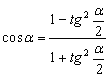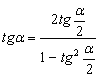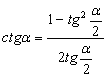|
5 класс:
6 класс:
7 класс:
8 класс:
Таблицы:
Популярные разделы:
Полезные материалы:
|
|
Тригонометрические формулы применяются при тождественных преобразованиях тригонометрических выражений, так и при доказательстве различных тригонометрических тождеств и соотношений. Знание основных тригонометрических формул просто необходимо всем изучающим математику.
Тригонометрические формулы, которые задают связь между между тригонометрическими функциями одного и того же аргумента, вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности. С помощью этих формул вы можете выразить одну тригонометрическую функцию через другую.
Тригонометрические формулы суммы и разности углов выражают сумму или разность углов через тригонометрические функции этих углов. Из этих формул, на основании формул суммы, вытекают тригометрические формулы двойного, тройного и половинного аргумента.
Тригонометрические формулы понижения степени используются для перехода от натуральных степеней синуса, косинуса, тангенса и котангенса к тригонометрическим функциям кратных углов первой степени.
Используя тригонометрические формулы преобразования произведения в сумму можно перейти от произведения тригонометрических функций к сумме или разности. И наоборот, применяя формулы преобразования суммы и разности тригонометрических функций в произведение, вы можете упростить тригонометрические выражения.
|
|