| Автор |
Сообщение |
Руслан
Гость

|
 Добавлено:
Сб Янв 09, 2010 1:16 pm Добавлено:
Сб Янв 09, 2010 1:16 pm |
  |
я нихрена незнаю,ети два задания мне дал препод,сказал что они меня спасут от вылета с ВУЗа...очень нужна ваша помощь...
№1
ДОведіть,що функції F(X) i δ(X) при х->0 є нескінченно малими одного порядку малості: F(x)=(корінь з 1+х) -1, δ(Х)= 2х.
№2
Обчисліть границі типів ![[1^{\infty }] [0^{0}] [\infty ^{0}]](http://latex.codecogs.com/gif.latex?[1^{\infty }] [0^{0}] [\infty ^{0}]) і lim (x->1) (1-x) (в степені) sin(Пі)х............ і lim (x->1) (1-x) (в степені) sin(Пі)х............
ПОМОГИТЕ ПОЖАЛУСТА,ЗСПАСИТЕ ДУШУ... |
|
|
|
 |
|
|
 |
Руслан
Гость

|
 Добавлено:
Сб Янв 09, 2010 11:53 pm Добавлено:
Сб Янв 09, 2010 11:53 pm |
  |
ну поможіть,тож пожалуста,чьо ви такі черстві... |
|
|
|
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Вс Янв 10, 2010 2:34 am Добавлено:
Вс Янв 10, 2010 2:34 am |
  |
Не черствые... Просто какой же из Вас специалист будет, если пара примеров уровня 2+2 отделяют Вас от исключения?.. Помочь-то можно... Но дальше тяжелее будет... Поищите, в интернете много хороших учебников и решебников, если хотите, могу посоветовать некоторые из них...
 |
|
|
  |
 |
Руслан
Гость

|
 Добавлено:
Вс Янв 10, 2010 12:33 pm Добавлено:
Вс Янв 10, 2010 12:33 pm |
  |
если можно подскажы книги,просто я пробалаболил ети темы,там ситуацыя была одна... |
|
|
|
 |
NonCommalg

Зарегистрирован: 06.09.2009
Сообщения: 21

|
 Добавлено:
Вс Янв 10, 2010 2:31 pm Добавлено:
Вс Янв 10, 2010 2:31 pm |
  |
В последнем примере, если надо без лопиталя, тогда так:
^{\sin \pi x}} = \left\{ \begin{gathered} x = 1 - t, \hfill \\ x \to 1, \hfill \\ t \to 0 \hfill \\ \end{gathered} \right\} = \mathop {\lim }\limits_{t \to 0} {t^{\sin \pi t}} = \mathop {\lim }\limits_{t \to 0} \exp \left\{ {\sin \pi t \cdot \ln t} \right\} = \hfill \\ = \exp \left\{ {\pi \cdot \mathop {\lim }\limits_{t \to 0} \frac{{\sin \pi t}} {{\pi t}} \cdot \mathop {\lim }\limits_{t \to 0} t\ln t} \right\} = \exp \left\{ {\pi \cdot 1 \cdot 0} \right\} = {e^0} = 1. \hfill \\ \end{gathered}) |
|
|
  |
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Вс Янв 10, 2010 4:46 pm Добавлено:
Вс Янв 10, 2010 4:46 pm |
  |
| NonCommalg писал(а): | | В последнем примере, если надо без лопиталя, тогда так: |
А разве это 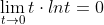
очевидно?  |
|
|
  |
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Вс Янв 10, 2010 4:51 pm Добавлено:
Вс Янв 10, 2010 4:51 pm |
  |
| Руслан писал(а): | | если можно подскажы книги,просто я пробалаболил ети темы,там ситуацыя была одна... |
Для начала возьмите первый том Каплан, "Практические занятия по высшей математике". Там пределы хорошо расписаны и объяснены. Если трудности с элементарной математикой, то можно взять Выгодского "Справочник по элементарной математике". Если вам удобнее читать на украинском, то одновременно с Каплан неплохо почитать Дубовик, Юрик "Вища математика". На первое время этого хватит, если что - обращайтесь )) |
|
|
  |
 |
Alexander
Site Admin

Зарегистрирован: 04.11.2006
Сообщения: 542
Откуда: Киев

|
 Добавлено:
Вс Янв 10, 2010 6:02 pm Добавлено:
Вс Янв 10, 2010 6:02 pm |
  |
| Цитата: | А разве это 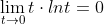 очевидно? очевидно? |
NonCommalg, кстати, совсем не очевидно, объясните... |
|
|
   |
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Вс Янв 10, 2010 11:20 pm Добавлено:
Вс Янв 10, 2010 11:20 pm |
  |
Там если без Лопиталя, можно, по идее, а ряд Тейлора логарифм разложить, и исходя из этого, посчитать предел. Взять в разложении первые два-три элемента и остаток, вроде норм должно получиться. |
|
|
  |
 |
NonCommalg

Зарегистрирован: 06.09.2009
Сообщения: 21

|
 Добавлено:
Пн Янв 11, 2010 12:31 am Добавлено:
Пн Янв 11, 2010 12:31 am |
  |
| Wolfling писал(а): | | NonCommalg писал(а): | | В последнем примере, если надо без лопиталя, тогда так: |
А разве это 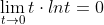
очевидно?  |
| Alexander писал(а): | | Цитата: | А разве это 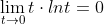 очевидно? очевидно? |
NonCommalg, кстати, совсем не очевидно, объясните... |
Ну один из пределов из основной таблицы:
) |
|
|
  |
 |
Wolfling
Moderator
Зарегистрирован: 25.10.2009
Сообщения: 118

|
 Добавлено:
Пн Янв 11, 2010 12:58 am Добавлено:
Пн Янв 11, 2010 12:58 am |
  |
А в таблицу он попал с помощью правила Лопиталя ?  |
|
|
  |
 |
|
|


